
|
|
|||||||
Hỏi một bài về khảo sát hàm số.this thread has 6 replies and has been viewed 5865 times
|

 |
|
|
Ðiều Chỉnh | Xếp Bài |
|
|
#1 |
|
Cho 1 hàm số f(x) bậc ba có chứa tham số m .
Xác định m để Ox cắt đồ thị hàm tại 3 điểm lập thành cấp số cộng. Cách làm thấy trong sách là gọi x1,x2,x3 là 3 nghiệm của pt f(x)=0. Giải hệ 2 pt x1+x2+x3=-b/a(Viete) x1+x3=2*x2. Suy ra x2 thế vào f(x)=0 để tìm tham số m rồi thử lại để chọn giá trị m thích hợp. Em lúc làm bài này có suy nghĩ thế này:hàm số bậc 3 có điểm uốn là tâm đối xứng suy ra f(x)=0 muốn có 3 nghiệm lập thành CSC thì nó phải qua điểm uốn.Từ đó,ta sẽ giải f"(x)=0 để tìm ngay ra nghiệm mà ko cần qua hệ.Khi thực hiện cách này trên 1 số hàm thì được kết quả chính xác,ko bị thiếu nghiệm. Như vậy,có thể mở rộng bài toán thành thế này: Cho 1 hàm f(x) bậc n lẻ chứa tham số m và trục hoành (Hoặc cho 1 hàm f(x) bậc lẻ cố định và 1 đường thẳng chứa tham số m.) Xác định m để đường này cắt f(x) tại n điểm lập thành CSC. Ta sẽ tìm đạo hàm cấp n-1 của f(x) rồi thế đạo hàm này vào pt đường thẳng,khi đó ta sẽ tìm được m. Cách làm như thế đúng ko?ACE có ý kiến.  
__________________
"hcmiu.edu.vn" thay đổi nội dung bởi: khanhan2006_2009, 04-09-2008 lúc 06:43 PM. |
|
|
|

|
| Đã có 2 thành viên gửi lời cám ơn đến khanhan2006_2009 vì bạn đã đăng bài: |
chinhlh (04-09-2008),
Stevvinhith (15-09-2015)
|
|
|
#2 |
|
Cách làm này sai hoàn toàn. Ngay cách làm bài bậc 3 ở trên của e cũng chưa được cm tính đúng đắn. Chỉ may mắn là trúng thôi. E thử áp dụng cách của e với bài này xem sao: X^4-X^2=0

__________________
Sống là chiến đấu!!!Chiến đấu cho cái đẹp! Quyết chiến đến cùng! Lê Quí Đôn là kỉ niệm và tình yêu!!! |
|
|
|

|
|
|
#3 |
|
Anh TC ui! Em nó đang đề cập đến hàm số bậc lẻ mà!
__________________
Necessity is the mother of in(ter)vention. Speak softly & carry a big stick. My Technical Blog |
|
|
|

|
|
|
#4 |
|
Vậy thì thử x^5-x^3=0 xem sao!!!??? Trong Toán cho ví dụ cm mệnh đề sai thật ko dễ!!!

__________________
Sống là chiến đấu!!!Chiến đấu cho cái đẹp! Quyết chiến đến cùng! Lê Quí Đôn là kỉ niệm và tình yêu!!! |
|
|
|

|
| Đã có thành viên gửi lời cám ơn đến lovelqd vì bạn đã đăng bài: |
Stevvinhith (15-09-2015)
|
|
|
#5 | |
|
Hehe,em đang đề cập đến hàm bậc lẻ..
Trích:
Chiều thuận:Nếu Ox qua điểm uốn I và hàm số f(x) có 2 cực trị thì hiển nhiên Ox sẽ cắt hàm số tại 3 điểm lập thành CSC do I là tâm đói xứng. Đảo lại:Giả sử có một điểm Q thuộc đồ thị f(x) sao cho Ox qua Q cũng cắt f(x) tại 3 điểm lập thành CSC.Ta chọn Q thuộc phần đồ thị nằm giữa 2 cực trị. Gọi A là điểm thuộc đồ thị như hình vẽ.Gọi A1 là đối xứng của A qua Q. Gọi A2 là điểm đối xứng A qua điểm uốn I. Khi đó ta có IQ song song A1A2=>vô lý. Tóm lại:đường qua điểm uốn I là duy nhất. 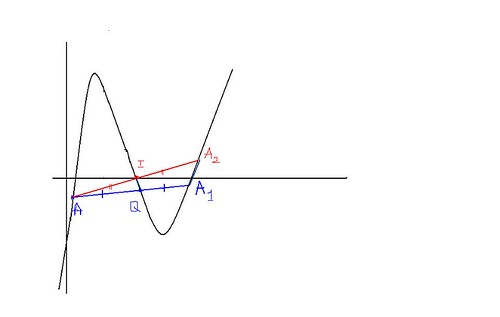 (ACE xem hình vẽ).
__________________
"hcmiu.edu.vn" thay đổi nội dung bởi: myhanh, 04-09-2008 lúc 10:38 PM. Lý do: Sửa đường liên kết hình |
||
|
|

|
|
|
#6 |
|
Trích:
__________________
Sống là chiến đấu!!!Chiến đấu cho cái đẹp! Quyết chiến đến cùng! Lê Quí Đôn là kỉ niệm và tình yêu!!! |
|
|
|

|
| Đã có thành viên gửi lời cám ơn đến lovelqd vì bạn đã đăng bài: |
Stevvinhith (15-09-2015)
|
|
|
#7 |
|
lâu lắm mới xem một bài viết mang tính ''học thuật'' như vầy. anh em phát huy nhe
__________________
Phong sương mấy độ qua đường phố Hạt bụi nghiêng mình nhớ đất quê |
|
|
|

|
 |
«
Ðề Tài Trước
|
Ðề Tài Kế
»
|
|
 Chủ đề tương tự
Chủ đề tương tự
|
||||
| Ðề tài | Người Gởi | Chuyên mục | Trả lời | Bài mới gởi |
| Tỉm sách tham khảo trên mạng ở đâu? | fantomas | Khoa học Tự nhiên | 7 | 12-01-2011 12:34 AM |
| Cho em hỏi chừng nào có kết quả phúc khảo? | NguyenQuocBao | K08 | 51 | 25-07-2008 08:52 PM |
| Vấn đề phúc khảo ? | QuyetThang | ..:: Bản Tin Trường ::.. | 20 | 21-07-2008 04:53 PM |
| Du khảo chụp ảnh nghệ thuật mùa nước nổi | nobipotter | ..::CLB Nhiếp Ảnh::.. | 21 | 17-11-2007 02:00 PM |
| Qui LỆ MÔn PhÁi Vovinam | LeGiang | ..:: CLB Thể Thao ::.. | 11 | 22-11-2006 12:31 PM |





 Linear Mode
Linear Mode



